What is Thevenin's theorem?

Many electronic circuits contain a combination of batteries, resistors and make it very complicated. So simplifying these complex circuits we need Thevenin's Theorem.

This theorem states that it is possible to simplify any linear circuits, to an equivalent circuit with just a single voltage source and impedance in series with the load, no matter how complex they are.

Thevenin theorem statements

According to this theorem, any two-terminal linear network containing energy sources and impedances can be replaced by an equivalent circuit consisting of a voltage source (V_TH) in series with an impedance (R_TH).

Where (V_TH) is the open-circuit voltage between the terminals of the network and (R_TH) is the impedance measured between the terminals with all the energy sources replaced by their internal impedances.

Thevenin's equivalent circuit

To show Thevenin's equivalent circuit we consider a circuit with a complicated passive network driven by an energy source (V_s). The network contains three resistors (R₁, R₂, and R₃) and they are connected with a load (R_L).

This circuit will be replaced by an equivalent circuit with a voltage source (V_TH) called Thevenin's voltage and impedance (R_TH) called Thevenin's impedance.

To calculate Thevenin's voltage at first remove the load. When the load has removed the voltage across AB is equal to the voltage across the resistor (R₂). So the Thevenin's voltage is

$\small V_{TH}=IR_{2}=\frac{V_{s}R_{2}}{R_{1}+R_{2}}\left [ \therefore I= \frac{V_{s}}{R_{1}+R_{2}}\right ]$

Where I = The flow of current through the circuit when the load is removed.

Now to calculate Thevenin's impedance at first replace the energy sources with their internal impedance and the load (R_L) also disconnected.

Note: If the internal impedance of the energy sources is given then it will be added to the resistor network.

Here the internal impedance is zero so the Thevenin's impedance is

$\small R_{TH}=R_{3}+R_{1}\parallel R_{2}$

$\small R_{TH}=R_{3}+\frac{R_{1}R_{2}}{R_{1}+R_{2}}$

Therefore the Thevenin's equivalent circuit for the above circuit is

Here the load current for this equivalent circuit is

$\small I_{L}=\frac{V_{TH}}{R_{TH}+R_{L}}$

Steps to follow for solving problems by Thevenin's Theorem

Step 1 :

Identify the load (R_L).

Step 2 :

Remove the load and calculate the open-circuit voltage (V_TH).

Step 3 :

To calculate Thevenin's impedance (R_TH), replace the sources with their internal impedance.

Step 4 :

Construct the Thevenin's equivalent circuit by connecting (V_TH) in series with (R_TH).

Solved problems by Thevenin's Theorem

Example 1: Calculate the current through the resistor of resistance 6 Ω.

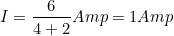
Solution :

To identify the load :

Here the load (R_L) = 6 Ω

To calculate Thevenin's voltage (V_TH) :

Now remove the load. When the load is removed the open-circuit voltage is the same as that of the voltage across the resistor of resistance 4 Ω.

∴ The current in the circuit is

$\small I=\frac{6}{4+2}Amp=1Amp$

∴ The Thevenin's voltage is

$\small V_{TH}=4\times 1=4V$

To calculate Thevenin's impedance (R_TH) :

After replacing the source with their internal impedance the Thevenin's impedance is

$\small R_{TH}=\left [ 2+2\parallel 4 \right ] =\left [ \frac{2\times 4}{2+4}+2 \right ] =\left [ \frac{4}{3}+2 \right ] =\frac{10}{3}\Omega =3.34\Omega$

Thevenin's equivalent circuit :

∴ The current through the load,

$\small I_{L}=\frac{4}{6+3.34}=\frac{4}{9.34}=0.43Amp$

Example 2: Calculate Thevenin's voltage and Thevenin's resistance.

Solution :

To calculate Thevenin's voltage (V_TH) :

Here the open-circuit voltage is the same as that of the voltage across the resistor of resistance 7 Ω.

∴ The current in the circuit is

$\small I=\frac{12}{3+7+2}=\frac{12}{12}=1Amp$

∴ The Thevenin's voltage is

$\small V_{TH}=1\times 7=7V$

To calculate Thevenin's impedance (R_TH) :

After replacing the source with their internal impedance the Thevenin's impedance is

$\small R_{TH}=\left [ \left ( 3+2 \right )\parallel 7 \right ]+3+3=\left \{ 5\parallel 7 \right \}+6=\frac{5\times 7}{5+7}+6=\frac{35}{12}+6=\frac{107}{12}=8.92\Omega$

Example 3: Calculate the current through the load resistance (R_L) = 5 Ω.

Solution :

To identify the load :

Here the load (R_L) = 5 Ω

To calculate Thevenin's voltage (V_TH) :

Now remove the load. When the load is removed the open-circuit voltage is the same as that of the voltage across the resistor of resistance 10 Ω.

Here the current through the first loop is

$\small I_{1}=\frac{V_{S}}{R_{1}}=\frac{20}{\frac{80}{11}}=\frac{20\times 11}{80}=\frac{11}{4}=2.75Amp$

Where

$\small R_{1}=\left [ \left ( 8+10 \right ) \parallel 4\right ]+4=\frac{18\times 4}{18+4}+4=\frac{36}{11}+4=\frac{80}{11}\Omega$

And the current through the second loop is

$\small I_{2}=\frac{4\times I_{1}}{R_{2}}=\frac{4\times 2.75}{22}=\frac{11}{22}=\frac{1}{2}=0.5Amp$

Where

$\small R_{2}=8+10+4=22$

∴ The Thevenin's voltage is

$\small V_{TH}=0.5\times 10=5V$

To calculate Thevenin's impedance (R_TH) :

After replacing the source with their internal impedance the Thevenin's impedance is

$\small R_{TH}=\left [ \left ( 4\parallel 4 \right ) +8\right ]\parallel 10=\left \{ \frac{4\times 4}{4+4} +8\right \}\parallel 10=\left ( 2+8 \right )\parallel 10=\frac{10\times 10}{10+10}=5\Omega$

Thevenin's equivalent circuit :

∴ The current through the load,

$\small I_{L}=\frac{5}{5+5}=\frac{1}{2}=0.5Amp$

Follow Us:

Thevenin theorem with solved problems

What is Thevenin's theorem?

Thevenin theorem statements

Thevenin's equivalent circuit

Solved problems by Thevenin's Theorem

Contact Form